
Acoustic Boundary Element Solver.

Dr Dan J. O’Boy
http://www.djoboy.co.uk
R1

Acoustic Boundary Element Solver.

Dr Dan J. O’Boy
http://www.djoboy.co.uk
R1
|
All rights reserved.
This manual is provided for reference and may not be copied and / or altered without the permission of the author. References to the manual should be made whenever material is used.
The manual provides guidance and information in order to use the Sonitus BE program and may be altered without notice being provided. No responsibility is assumed or given for any damage, commitments, liabilities or inaccuracies incurred as a result of the information provided.
All material is the intellectual property of this company through the owner Dr Dan J. O'Boy, who applies the property rights. The terms and conditions are applied through and in accordance with English law and any disputes will be subject to the jurisdiction of the courts of England and Wales of the United Kingdom.
|
Revision 1
Copyright ©2008
Dr Dan J O’Boy
4 The Green
Exton
Oakham
Rutland
LE158AP
United Kingdom
enquires@djoboy.co.uk
A typical boundary element code has several advantages over traditional finite differencing calculation methods. As with finite element codes, a geometry is described and a mesh generated, however, only the bounded surfaces require meshing, which allows not just a speed advantage, but also the possibility to investigate domains which are relatively large in comparison to the geometry being examined.
Broadly speaking, boundary conditions are applied to the surface under investigation, and solutions found for the amplitude of potentials applied to the surface which yield those boundary conditions. Once these amplitudes are known, they may be used to obtain the displacement, velocity or other parameter inside the domain.
The aim of this section is to provide an illustration of the boundary element method, through the work of Brebbia and Walker. [C. A. Brebbia, “The Boundary Element Method for Engineers”. Pentech Press, 1980. C. A. Brebbia and S. Walker, “Boundary Element Techniques in Engineering, Newnes-Butterworths, 1980].

Figure 5 Definition of a domain for acoustic calculations.
A domain is defined by the symbol ![]() and a surface which is closed inside it
and a surface which is closed inside it ![]() . This surface is separated into two
sections, joined together to create a closed surface, with the first section
denoted
. This surface is separated into two
sections, joined together to create a closed surface, with the first section
denoted ![]() and
the second
and
the second ![]() as
shown in Figure 5. On each surface are located surface potentials of unknown
amplitude which give rise to certain physical conditions on the surface.
as
shown in Figure 5. On each surface are located surface potentials of unknown
amplitude which give rise to certain physical conditions on the surface.
On the first, ![]() , for the acoustic calculation is a term
, for the acoustic calculation is a term ![]() while
in on the surface
while
in on the surface ![]() we
define the property of interest to be the normal derivative, the flux
we
define the property of interest to be the normal derivative, the flux ![]() . It is possible to
write the physical boundary conditions of pressure or velocity in terms of the
amplitudes of the fundamental solutions.
. It is possible to
write the physical boundary conditions of pressure or velocity in terms of the
amplitudes of the fundamental solutions.
By converting physical conditions such as pressure or velocity into just the amplitudes of the fundamental solutions, the problem can be decomposed into a generic solution to a matrix.
The exact solutions for the physical properties are denoted
by the functions ![]() and
and
![]() on the
sections of the surface respectively. This allows an error on the surfaces to be defined as,
on the
sections of the surface respectively. This allows an error on the surfaces to be defined as,
|
|
on |
|
|
on |
|
|
|
The aim of the boundary element method is to determine the
amplitude of a distribution of potentials so as to minimise the error. This error is distributed over the surface according to a weighting function ![]() ,
which may be a fundamental solution to the governing equation in the domain.
,
which may be a fundamental solution to the governing equation in the domain.
The distribution of the error in the domain is written,
 .
.
For the Helmholtz problem, the governing equation is ![]() , where the
wavelength is denoted
, where the
wavelength is denoted ![]() . Substitution of the error residuals and weightings (fundamental solutions) provides the starting weighting residual statement.
. Substitution of the error residuals and weightings (fundamental solutions) provides the starting weighting residual statement.

where ![]() describes the fundamental solution to
the Helmholtz equation,
describes the fundamental solution to
the Helmholtz equation, ![]() (also termed the Green’s function).
(also termed the Green’s function).
The first term may be integrated by parts,

It is noted that we have specified that the boundary conditions on the two parts of the surface must exactly meet the exact solution. Therefore, this simplifies the equation to,
![]()
The integration over the domain of the fundamental solution yields only a delta term, located at the point of interest “i”.
![]()
This final equation relates the value of ![]() at the location of point “i”
with the values of
at the location of point “i”
with the values of ![]() and
and ![]() over the domain
over the domain ![]() and it applies when the
point is inside the interior domain
and it applies when the
point is inside the interior domain ![]() . The advantage of boundary integrals appears when we only consider points on the surface of the geometry, therefore the point needs to be moved to this boundary. Due to the
singularity which occurs at this point, we analytically represent this through
a constant
. The advantage of boundary integrals appears when we only consider points on the surface of the geometry, therefore the point needs to be moved to this boundary. Due to the
singularity which occurs at this point, we analytically represent this through
a constant ![]() .
For a point inside the boundary,
.
For a point inside the boundary, ![]() , for a point on the boundary it is 0.5
and outside the boundary it is zero.
, for a point on the boundary it is 0.5
and outside the boundary it is zero.

This is the governing boundary element equation for use with a fundamental Helmholtz solution. Such solutions for the fundamental equation are shown in Table 5.
The boundary element equation is a continuous integral, however the numerical implementation is a discrete equation with truncation errors through the continuous domain being represented by a series of linear joins, as shown in Figure 6. The requirements for this discretisation, the type of elements which can be created and the number of elements for a given acoustic frequency are discussed later in this manual.
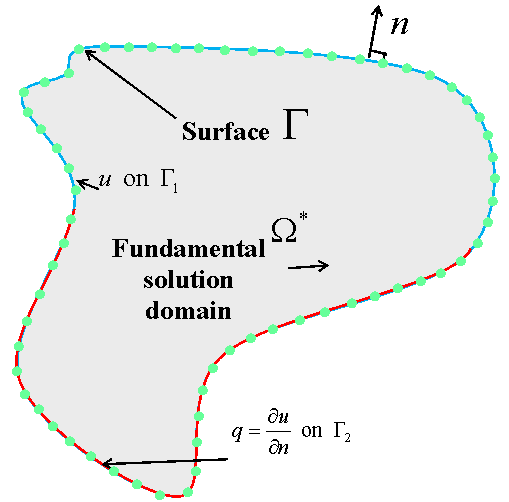
Figure 6 Discretisation of the surface bounding the solution domain. The surface is created by joining nodes together with linear segments. When completed over a three dimensional domain, the linear segments create surface areas (elements).
The formulation of the indirect boundary element method
starts with the boundary integral equation ![]() applied to an interior domain
applied to an interior domain ![]() .The indirect method
starts with a solution which satisfies the governing equation in the domain but
has unknown coefficients at a number of points. At this point, we also
introduce to the formulation a monopole source located inside the domain which
will allow the non-trivial solution to be obtained (without this, the only
sound field that exists is silence). The amplitude of this source is
.The indirect method
starts with a solution which satisfies the governing equation in the domain but
has unknown coefficients at a number of points. At this point, we also
introduce to the formulation a monopole source located inside the domain which
will allow the non-trivial solution to be obtained (without this, the only
sound field that exists is silence). The amplitude of this source is ![]() with a location inside
with a location inside
![]() .
.
![]()
As shown in Figure 6, the surface can either be integrated as a continuous surface (we will use the continuous form for the present section) or discretised by nodes joined with linear elements.
In order to enforce the boundary condition on the surface,
it becomes necessary to also consider a domain exterior to the surface ![]() where no sources
exist and the properties
where no sources
exist and the properties ![]() are governed by the equation
are governed by the equation ![]() (as the surface is
pointing in the opposite direction, the sign is reversed).
(as the surface is
pointing in the opposite direction, the sign is reversed).
As part of the derivation, we assume that the solution generated for the exterior field is identical to that generated for the interior field on the surface. Therefore we are able to write,
![]()
On the surface, it is possible to write that ![]() as exact terms.
Rearranging the above equation, these terms cancel with each other.
as exact terms.
Rearranging the above equation, these terms cancel with each other.

If we examine the form of this equation, we can define ![]() as the unknown
density of the fundamental solutions or amplitudes of the fundamental solutions
across the surface of the domain, necessary to generate
as the unknown
density of the fundamental solutions or amplitudes of the fundamental solutions
across the surface of the domain, necessary to generate ![]() The constants can be taken
inside this variable and summarised as,
The constants can be taken
inside this variable and summarised as,

An alternative formulation is clearly gained by writing the
sum of the derivatives of u, the fluxes as equal to zero. If ![]() then the boundary
integral equation becomes
then the boundary
integral equation becomes
Writing the dipole term ![]() relates the value of
relates the value of ![]() in the domain to
the amplitude of a series of dipoles distributed over the whole surface.
in the domain to
the amplitude of a series of dipoles distributed over the whole surface.

The former method has greater advantages as lower orders of
derivatives of the fundamental solution are utilised. If we choose this former
method, then we can write ![]() and the derivative, the flux, as,
and the derivative, the flux, as,

This applies for any point on the inside of the domain,
however, in order to find the value of a point on the boundary, the location ![]() needs to be moved to
the surface. A singularity exists, therefore, the integration is carried out
analytically, to obtain,
needs to be moved to
the surface. A singularity exists, therefore, the integration is carried out
analytically, to obtain,

Up until this point, the boundary integral equation has been considered as a continuous integral over the surface in the domain. There are a number of challenges with this method, most notably that few geometries exist in reality where there is simple analytical solution for the boundary integral. It is more likely that the geometry is a component in an automotive, aeronautical, aerospace or industrial environment.
For this reason, the integral has to be completed using a numerical method, which requires that the surface be discretised into a series of nominally evenly spaced nodes (see Figure 1 for a description of the node and Figure 6 to see how the surface is broken up into elements separated by these nodes).
There are ![]() elements from
elements from ![]() to
to ![]() , where we may describe two
different elements by their indices
, where we may describe two
different elements by their indices ![]() and
and ![]() . The value of
. The value of ![]() on element
on element ![]() is denoted
is denoted ![]() while the value
attached to element
while the value
attached to element ![]() is
is ![]() . We may then begin to write the
discretised formulation in matrix notation using a summation over
. We may then begin to write the
discretised formulation in matrix notation using a summation over ![]() elements. At this
point we do not consider the implications of
elements. At this
point we do not consider the implications of ![]() in the mathematical derivation. In
addition, we temporarily leave the source term
in the mathematical derivation. In
addition, we temporarily leave the source term ![]() out of the equations, for brevity.
out of the equations, for brevity.
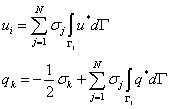
The boundary integrals are provided with their own specific
notation for the matrices, such that 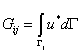 and
and  .
.
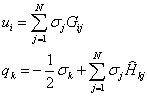
Finally, for the boundary integral for the fluxes, we may
write that if ![]() then
then
![]() , whereas
for
, whereas
for ![]() ,
, ![]() .
.

Now we introduce the discretisation of the source term.
These can be used to include either monopole sources or body forces. These are
written as ![]() .
.
Our final discretised indirect boundary integral equation is left as,

In this code, the matrices are hard coded for ![]() elements as
elements as ![]() .
.

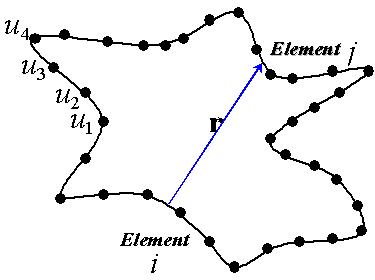 |
Figure 7 Boundary integral surface illustrating how each element takes into account the effect of a source of unknown amplitude located at each element. The problem is then posed as “what amplitude of all of the sources yields the correct known boundary condition at this element?” in matrix form.
The effect of each fundamental solution located at the nodes
are shown in Figure 7, where it may be seen that the vector ![]() is never zero, as two nodes
are never co-located.
is never zero, as two nodes
are never co-located.
The integration of the boundary element is usually the most complex part of the boundary element code, due to the fact that the surface is generally not aligned with the principle axes of the problem (see for example the example in any of the previous figures) but rather with the normals pointing in an arbitrary direction (yet consistent with each other).
In this document, two integral methods are shown as examples, relating to the integration of a quadrilateral and also triangular element respectively. Both element types are calculated in a similar manner.
The components of the matrix  , where the fundamental solution is
assumed to be o the form
, where the fundamental solution is
assumed to be o the form ![]() where the frequency in radians /
second is related to the frequency in Hz by
where the frequency in radians /
second is related to the frequency in Hz by ![]() and r is the distance between the
source element and the observer element. The element is defined using
non-dimensional coordinates and an interpolation routine is used to obtain the
values of the fundamental solution across the whole element. A linear integration
method is then applied to determine the value of the integration over the area
of the element.
and r is the distance between the
source element and the observer element. The element is defined using
non-dimensional coordinates and an interpolation routine is used to obtain the
values of the fundamental solution across the whole element. A linear integration
method is then applied to determine the value of the integration over the area
of the element.
The principle axes are ![]() , however the linear element may be
sloping in directions which are different to this. Therefore there needs to be
an integration along non-dimensional coordinates. This involves a change of
variable in the double integral using a Jacobian method.
, however the linear element may be
sloping in directions which are different to this. Therefore there needs to be
an integration along non-dimensional coordinates. This involves a change of
variable in the double integral using a Jacobian method.
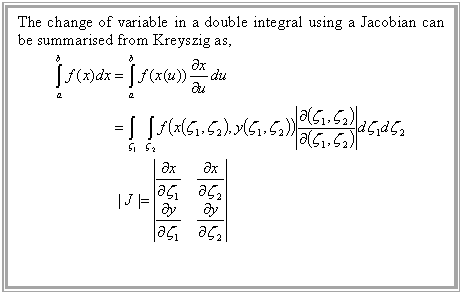
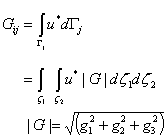
We now look at the element ![]() , with four labels denoting nodes k=1,
2, 3 and 4.
, with four labels denoting nodes k=1,
2, 3 and 4.
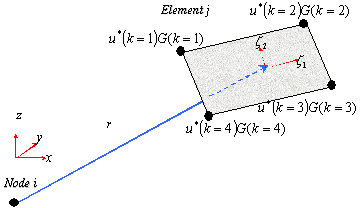
Figure 8 Quadrilateral boundary integral surface showing non-dimensional coordinate form of the surface direction.
For each coordinate node on the element,
the product ![]() is obtained, where the surface
directions are obtained through an interpolation routine (the details are
provided in the coding explanation).
is obtained, where the surface
directions are obtained through an interpolation routine (the details are
provided in the coding explanation).
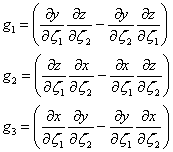
Once the product of ![]() is found at each of the corners, the
numerical integration can take place. For a linear surface, the following is
appropriate.
is found at each of the corners, the
numerical integration can take place. For a linear surface, the following is
appropriate.
Figure 9 Quadrilateral linear integration method.

This is Gauss’ integration method for linear elements in two dimensions (non-dimensionalised), See Abramowitz and Stegun P887, P916 for weightings .
So ![]() , where
, where ![]() . This is the final boundary integral
for the linear quadrilateral element.
. This is the final boundary integral
for the linear quadrilateral element.
The process is similar for triangular elements, first the
value of the fundamental solution is obtained between each node ![]() and nodes which make
up the three corners of the triangular element
and nodes which make
up the three corners of the triangular element ![]() , k=1,2,3.
, k=1,2,3.
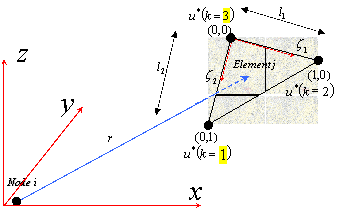
Figure 10 Triangular linear integration method.
The position of a point on the triangular element is,
![]()
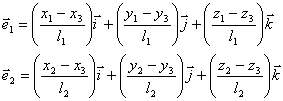
These are rearranged to obtain any point on the triangular element as a function of non-dimensional coordinates.
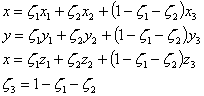
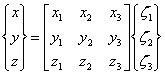
![]()
Once the values at an arbitrary location on the triangular element are known, the integration over the surface area can be found using a simple Gaussian integration method for triangular elements, where the non-dimensional coordinate varies from 0 to 1.
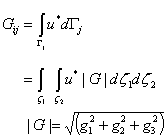
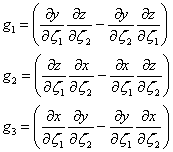
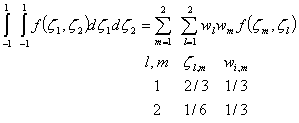
This is Gauss’ integration method for linear elements in two dimensions (non-dimensionalised), See Abramowitz and Stegun P887, P916 for weightings .
So ![]() , where
, where ![]() . This is the final boundary integral
for the linear triangular element.
. This is the final boundary integral
for the linear triangular element.
For a non-trivial solution, the domain needs to include at least one source, with defined amplitude Q and location. If the distance between the source and the observer element is given by Rs, then the pressure and velocity may be written in terms of this distance and the fundamental solution.
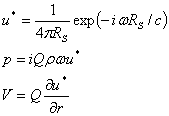
The data recovery points are incorporated into the input file as a list of points where the user is interested in knowing the acoustic pressure, intensity or velocity. They must be at least one quarter of an acoustic wavelength away from the solid geometry (boundary) in order to avoid singularities occurring in the boundary integral formulation.
The data recovery points can either be designed as single points or through the use of a meshing program, which allows a fuller graphical representation of the end data.
The preferred format for the data recovery mesh is through the use of a Patran Neutral file with extension “.out.1”. Although Patran is a commercial program, many converters exist for moving between one neutral format to another.
As a result, it is relatively easy to obtain the data recovery mesh in this appropriate format, however, it is also possible to directly program typical geometries into the correct surface mesh format through the use of a bespoke program. One such example is provided here, in the subdirectory “DRMGen”.
The Patran file format contains information about the location of the nodes making up the data recovery mesh, and also how they are connected to create a structured orderly design for graphical processing. A file may also include data on material properties and node loading, however these are not of interest for this application.
The scripted mesh generator provides a structured grid of quadrilateral elements with a fixed number in the x and y directions. It models a mesh surrounding an automotive tyre, see Figure 15 for an illustration. The first few lines of the file describe how many nodes are to be defined in the program and a date (and time) of creation.
The nodal data number is defined, followed by it’s position in three dimensional Cartesian coordinates, x,y,z. Following this, a list of the elements are defined. These quadrilateral elements connect four nodes together. As previously described, it is vital that the normal directions of conjoining elements be consistent.
The C++ data recovery mesh program can be compiled using the command “g++ DRMGen_Tyre.cpp –o a.out”.
Once the location of the data recovery nodes are known it
remains to determine the physical parameters of interest. We start with the
equation for the known boundary condition relating to the matrix of boundary
integrals and their associated amplitudes ![]() . At this point we assume that we have
a suitable solution for the amplitudes
. At this point we assume that we have
a suitable solution for the amplitudes ![]() , which will allow all physical
parameters to be determined inside the domain.
, which will allow all physical
parameters to be determined inside the domain.
If the amplitudes of the fundamental solutions are known
across the surface, as shown in Figure 11, then the corresponding boundary
integrals can be calculated between each data recovery node and each boundary
element on the surface. This is written as, ![]() .
.
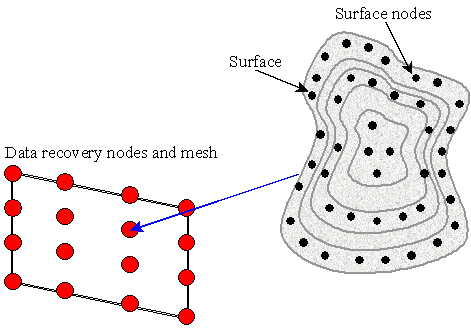
Figure 11 Boundary integrals from the surface to the data recovery mesh.
In order to obtain the pressure and velocity at each data recovery point, the relationship between the fundamental solution and these physical relations are re-stated.
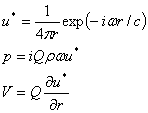
The pressure may be calculated at each of the data recovery
points thus,![]() as the amplitude of the source (usually Q) is given by
as the amplitude of the source (usually Q) is given by ![]() . In addition to this, the
contribution from the source location is also added.
. In addition to this, the
contribution from the source location is also added.
The output variables relating to the sound pressure are denoted for the i’th node: Outputvar[i][0] to Outputvar[i][2].
Outputvar[i][0] Sound pressure in dB re Pref.
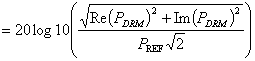
Outputvar[i][1] Sound pressure magnitude [N/m^2].
![]()
Outputvar[i][2] Sound pressure phase in degrees.
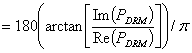
The velocity is given by ![]() where r is the distance from the
source element to the observer data recovery node. The velocity is different
from the pressure in that the former is a scalar whereas the velocity can be
defined in terms of components in the three Cartesian axes.
where r is the distance from the
source element to the observer data recovery node. The velocity is different
from the pressure in that the former is a scalar whereas the velocity can be
defined in terms of components in the three Cartesian axes.
![]()
Outputvar[i][3] X component of the velocity, magnitude [m/s].
![]()
Outputvar[i][5] Y component of the velocity, magnitude [m/s].
![]()
Outputvar[i][7] Z component of the velocity, magnitude [m/s].
![]()
Outputvar[i][9] Magnitude of the velocity, magnitude [m/s].
![]()
Outputvar[i][4] X component of velocity, phase [degrees].
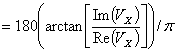
Outputvar[i][6] Y component of velocity, phase [degrees].

Outputvar[i][8] Z component of velocity, phase [degrees].
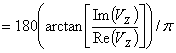
The acoustic intensity can be determined for each of these
coordinate axes through the power dissipation analogy in electrical components.
The intensity may be written in terms of the pressure and velocity using ![]() where the overbar
denotes the complex conjugate.
where the overbar
denotes the complex conjugate.
Outputvar[i][10] X component of the intensity.
![]()
Outputvar[i][11] Y component of the intensity.
![]()
Outputvar[i][12] Z component of the intensity.
![]()
Two numerical methods are available for the solution of an matrix problem, however, the computer code has been written so that a different solution method may be substituted with no significant alteration required. The two methods are Gaussian Jordan and LU decomposition, both validated through the use of complex value matrices.
The method is based on the classical equation ![]() where the vector of
boundary conditions and sound source contributions are given by
where the vector of
boundary conditions and sound source contributions are given by ![]() (known), the
amplitudes of the fundamental solutions
(known), the
amplitudes of the fundamental solutions ![]() (unknown) and the square matrix of
boundary integrals
(unknown) and the square matrix of
boundary integrals![]() (known).
(known).
In the code, these variables are copied into duplicated
variables for processing. The solution function is then called, which replaces
the square matrix ![]() with
with
![]() and the
vector
and the
vector ![]() with
with
![]() .
.
Details of solution methods are available in Flowers, “An Introduction to Numerical Methods in C++”, Clarendon Press, Oxford, 1995.
The Gauss-Jordan elimination is not the most efficient
solver, however, is well known and many varieties of the code exist. It differs
from a standard Gauss solver as back substitution to reduce a matrix to a
triangular form is avoided. Instead, additional operations reduce the matrix to
diagonal formation. It is assumed that the matrix ![]() is non-singular with a well defined
inverse.
is non-singular with a well defined
inverse.